How far in advance are flights cheapest? An error of interpretation
Posted on Wed 06 January 2016 in TDDA
Guest Post by Patrick Surry, Chief Data Scientist, Hopper
Every year, Expedia and ARC collaborate to publish some annual statistics about domestic airfare, including their treatment of the perennial question "How far in advance should you book your flight?" Here's what they presented in their report last year:
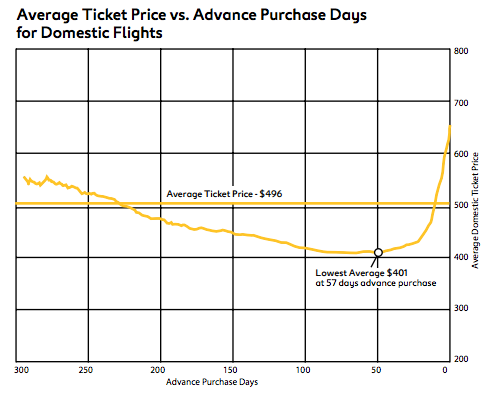
Although there are a lot of things wrong with this picture (including the callout not being at the right spot on the x-axis, and the $496 average appearing above $500 . . .), the most egregious is a more subtle error of interpretation. The accompanying commentary reads:
Still, the question remains: How early should travelers book? . . . Data collected by ARC indicates that the lowest average ticket price, about US$401, can be found 57 days in advance.
While that statement is presumably mathematically correct, it's completely misleading. The chart is drawn by calculating the average price of all domestic roundtrip tickets sold at each advance. That answers the question "how far in advance is the average ticket sold on the day lowest?" but is mistakenly interpreted as answering "how far in advance is a typical ticket cheapest?". That's a completely different question, because the mix of tickets changes with advance. Indeed, travelers tend to book more expensive trips earlier, and cheaper trips later. In fact, for most markets, prices are fairly flat at long advances, and then rise more or less steeply at some point before departure. As a simplification, assume there are only two domestic markets, a short, cheap trip, and a long, expensive one. Both have prices that are flat at long advances, and which start rising about 60 days before departure:
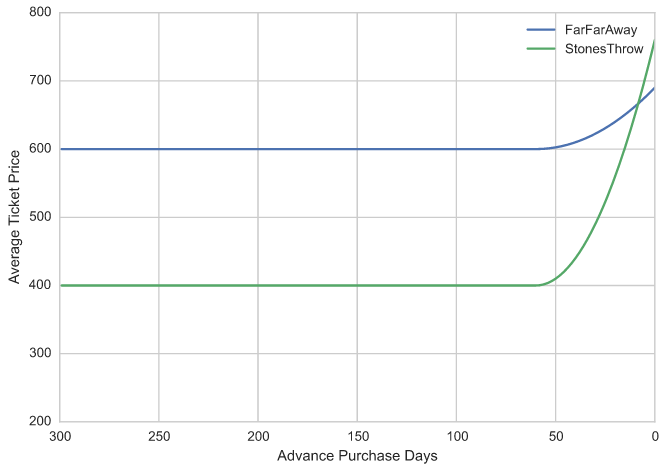
Now let's assume that the relative demand is directly proportional to advance, i.e. 300 days ahead, all tickets sold are for FarFarAway, and 0 days ahead, all tickets sold are for StonesThrow, and let's calculate the price of the average ticket sold as a function of advance:
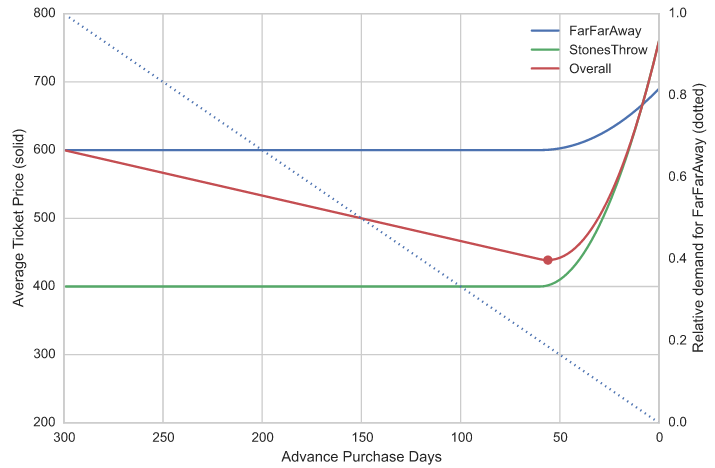
What do you know? The average price declines as demand switches from more expensive to cheaper tickets, with a minimum coincidentally just less than 60 days in advance. To get a more meaningful answer to the question "how far in advance is the typical ticket cheapest?", we should instead simply calculate separate advance curves for each market, and then combine them based on the total number (or value) of tickets sold in each market. In our simple example, if we assume the two markets have equal overall weight, we get a much more intuitive result, with prices flat up to 60 days, and then rising towards departure:
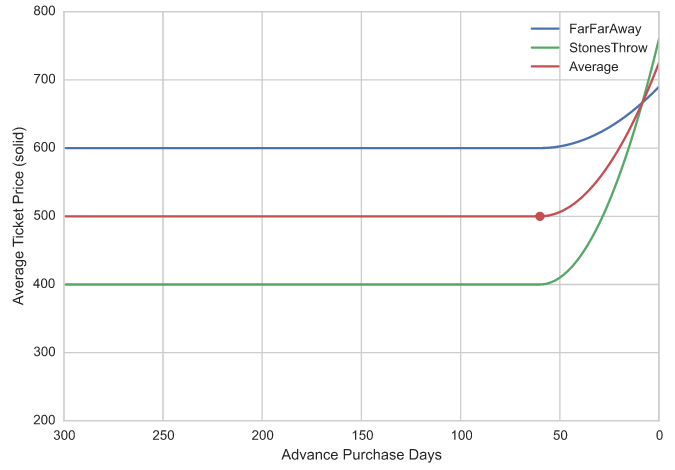
All this goes to show how important it is that we frame our analytical questions (and answers!) carefully. When the traveller asks: "How far in advance should I book my flight?", it's our responsibility as analysts to recognize that they mean
How far in advance is any given ticket cheapest?
rather than
How far in advance is the average price of tickets sold that day lowest?
Even a correct answer to the latter is dangerously misleading because the traveller is unlikely to recognize the distinction and take it as the (wrong!) answer to their real question.